K-means Clustering in R

K-means is a clustering technique that uses similarity to divide a set of data points into K groups. It operates by allocating each data point repeatedly to the cluster with the closest mean and then updating the mean of each cluster depending on the new assignments. When the cluster assignments no longer change, the algorithm ends.

The K-means algorithm is explained as follows:

• Determine the number of clusters K that you wish to find in the data.
• Create K centroids at random.
• Each data point should be assigned to the nearest centroid.
• Based on the updated assignments, update the cluster centroids.
• Steps 3 and 4 should be repeated until the cluster assignments no longer change.

The K-means algorithm has several essential characteristics, including:

• It is simple to comprehend and implement.
• It is computationally efficient and capable of dealing with huge datasets.
• It may be used to discover an appropriate starting point for various clustering techniques.

However, it has certain drawbacks, including:

• Depending on the initial placements of the centroids, the method may converge to a poor solution.
• The procedure assumes that the clusters are spherical, of similar size, and of equal density.
• The method may not perform well with datasets of varying shapes and densities.

Despite these restrictions, K-means is commonly used in modern world problems and has several applications in computer vision, marketing, and biology.

Various measures, such as the within-cluster sum of squares (WCSS) and silhouette score, can be used to assess the performance of a K-means model. The total of the squared distances between each data point and its assigned centroid inside each cluster is calculated using WCSS. The silhouette score, which runs from -1 to 1, quantifies how similar each data point is to its allocated cluster relative to the other clusters.

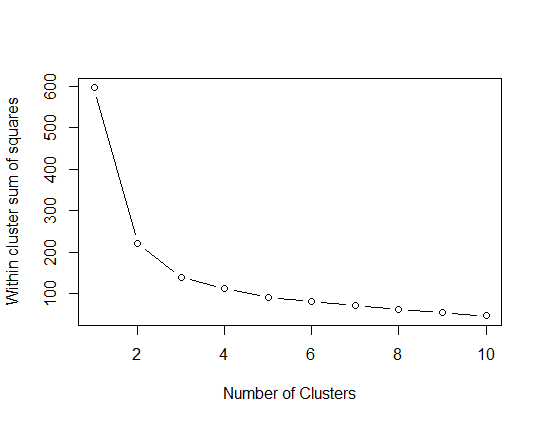
We can display the data points and centroids in a scatter plot to see the results of a K-means model, with each colour representing a distinct cluster. To assist us pick the best number of clusters, we may display the WCSS and silhouette score as a function of the number of clusters K.

Let's unleash the R-Code for K-Means!

Load the required packages

lbrary(cluster)
library(factoextra)
library(ggplot2) 

Load the dataset

data(iris)
X = iris[,1:4]

Preprocess the data

X_scaled = scale(X)
  

Find the optimal number of clusters using the elbow method

wss = c()
for (i in 1:10) {
  kmeans_fit = kmeans(X_scaled, centers = i, nstart = 10)
  wss[i] = kmeans_fit$tot.withinss
}
plot(1:10, wss, type = "b", xlab = "Number of Clusters", ylab = "Within cluster sum of squares")

Fit a K-means model with the optimal number of clusters

kmeans_fit = kmeans(X_scaled, centers = 3, nstart = 10)

Plot the results

fviz_cluster(list(data = X_scaled, cluster = kmeans_fit$cluster), 
                  geom = "point", palette = "jco", stand = FALSE) 
                  + ggtitle("K-means Clustering")

Summary

• We make use of the Iris dataset in this example. The data is first preprocessed by being scaled to have a zero mean and unit variance. 
• Next, we construct a K-means model with three clusters using the elbow technique to get the ideal number of clusters. 
• The fviz_cluster function from the "factoextra" package is then used to present the results. This function generates a scatter plot of the data points coloured according to their cluster assignment and overlays it with the cluster centroids.