Linear regression is a statistical method used to model the relationship between one or more independent variables and a dependent variable. The goal of linear regression is to find a linear relationship between the independent and dependent variables.
Linear regression is widely used in many disciplines, including business, science, and engineering. It can predict future trends and outcomes based on historical data and identify relationships between variables.
Linear regression is classified into two types: simple linear regression and multiple linear regression. There is only one independent variable in simple linear regression, whereas multiple independent variables exist in multiple linear regression.
The Boston dataset is about the housing values in the suburbs of Boston. This data frame contains the following variables:
- Crim - per capita crime rate by town.
- Zn - the proportion of residential land zoned for lots over 25,000 sq. ft.
- Indus - the balance of non-retail business acres per town.
- Chas - Charles River dummy variable (= 1 if tract bounds river; 0 otherwise).
- Nox - nitrogen oxides concentration (parts per 10 million).
- Rm - the average number of rooms per dwelling.
- Age - the proportion of owner-occupied units built prior to 1940.
- Dis - weighted mean of distances to five Boston employment centres.
- Rad - index of accessibility to radial highways.
- Tax - full-value property-tax rate per $10,000.
- Ptratio - pupil-teacher ratio by town.
- Black - where Bkis the proportion of blacks by city.
- Lstat - lower status of the population (percent).
- Medv - median value of owner-occupied homes in $1000s.
- We are importing it from the MASS package.
Let's see the analysis part.
Importing the Mass package which contains the Boston (Housing Values in Suburbs of Boston) dataset.
Scatterplot matrix
Correlation plot
library(MASS)
BostonFor further analysis, we split the dataset into train and test data by using randomization which will allocate the train and test variable randomly to the observations (as shown in the figure).
set.seed(2)
library(caTools)
split = sample.split(Boston$medv, SplitRatio = 0.7)## dividing the dataset into 70:30 Ratio
split
training_data = subset(Boston, split =="TRUE")
testing_data = subset(Boston, split =="FALSE")
library(lattice) ## Scatterplot matrix
splom(~Boston[c(1:6,14)], groups = NULL, data = Boston, axis.line.tck = 0, axis.text.alpha = 0)
cr = cor(Boston)
library(corrplot)
corrplot(cr, type = "full")
For the Multiple Linear Regression, we need to check for multicollinearity. Multicollinearity means the independent variables should be independent, it should not have a high relationship with the other variable. For that, we have to use the Variance Inflation Factor (VIF). The variance inflation Factor measures the increase in the variance of an estimated regression coefficient due to multicollinearity. The VIF values should be less than 5 is fine but if it is more than 5 it has the multicollinearity problem.
##VIF
library(car)
model = lm(medv~. , data = training_data)
vif(model)
#create vector of VIF values
vif_values = vif(model)
#create horizontal bar chart to display each VIF value
barplot(vif_values, main = "VIF Values", horiz = TRUE, col = "steelblue")
abline(v = 5, lwd = 3, lty = 2)Here, rad and tax have higher variance factor values indicating high multicollinearity. ra and tax are highly correlated at 0.91. Removing or reducing the multicollinearity has lots of methods but here we are simply removing the variable which is not that much important to predict the dependent. So we can remove one of the predictors (rad or tax) to remove multicollinearity. nox, indus and dis are moderately correlated.
model = lm(medv~crim+zn+chas+nox+rm+dis+ptratio+black+lstat, data = training_data)
summary(model)
In the above model, the tax is not affecting the Dependent variable which means it is less than 0.05. So We can take it out, but then we must refit the model.
model = lm(medv~crim+zn+chas+nox+rm+dis+ptratio+black+lstat, data = training_data)
summary(model)
prd = predict(model, testing_data) # predicting the test data
plot(testing_data$medv, type = "l", col = "green" )
lines(prd, type = "l", col = "blue")
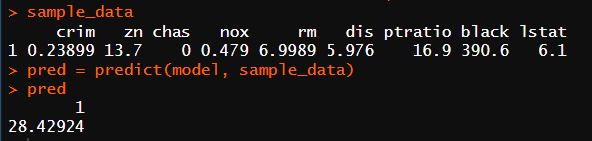
By using the above model we are predicting the sample data with random values:
sample_data = data.frame(crim = 0.23899, zn = 13.7,chas = 0, nox = 0.479, rm = 6.9989,
dis = 5.976,ptratio = 16.9, black = 390.6, lstat = 6.1)
sample_data
pred = predict(model, sample_data)
predConclusion
The regression model is fitted for the Boston dataset and we obtained the 0.7253 R-squared value. Sample data is also predicted with 72% accuracy by using the fitted model.
Reference
- Boston: Housing Values in Suburbs of Boston - RDocumentation.
- Harrison, D. and Rubinfeld, D.L. (1978) Hedonic prices and the demand for clean air. J. Environ. Economics and Management 5, 81–102.
- Belsley D.A., Kuh, E. and Welsch, R.E. (1980) Regression Diagnostics. Identifying Influential Data and Sources of Collinearity. New York: Wiley.